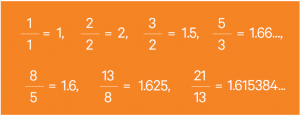For maths YouTube sensation Toby Hendy, inspiration definitely exists, but it has to find you walking.
This fascinating article explains how maths exists in many forms in the natural world, for example, flowers following the Fibonacci sequence to spread their petals and capture the most sunlight. It is best suited to Year 10 and Senior STEM students who are studying Biology or General Maths. It also covers some of the Numeracy sub-categories within the General Capabilities and so it could be used with younger students to discover real-world applications of patterns like the golden ratio and Fibonacci sequence.
Word Count: 1721
Walking is a wonderful activity. Sometimes we walk for practical reasons, to get from point A to point B, although if we’re constrained to footpaths we don’t often get to travel as the crow flies. The design of most city streets favours grid lines rather than the hypotenuse, and some meandering paths don’t favour straight lines at all. We may also walk as a way to explore or to energise the mind. When I walk, I leave my headphones at home – I’ve come to realise that some of my best ideas and inspired thoughts have come to me while my feet remain in motion and my mind’s not distracted. Any activity that allows our bodies to move can help to solidify connections between disparate thoughts. As our muscles move, more blood (and with it, oxygen) is pumped to all of our organs including the brain, where it can be gobbled up by our thinking – sometimes tackling deep questions about the nature of mathematics; other times focussed on what we should cook for dinner.
As someone who loves both science and walking, I am in good company. One notable discovery made while walking was that of quaternions: a number system that extends the complex numbers to four dimensions. The complex numbers, composed of a real and an imaginary part, describe points on a plane and can be multiplied together, giving a way to perform rotation in two dimensions. Mathematician Sir William Rowan Hamilton spent years fruitlessly searching for a way to extend the complex numbers to be able to rotate objects in three dimensions. Reminiscing on those days in a letter to his son Archibald, Hamilton wrote: “Every morning in [early October 1843], on my coming down to breakfast, your (then) little brother William Edwin, and yourself, used to ask me, ‘Well, Papa, can you multiply triplets?’ Whereto I was always obliged to reply, with a sad shake of the head: ‘No, I can only add and subtract them.’ ”
Not long after, on 16 October 1843, Hamilton was walking along the Royal Canal in Dublin with his wife when he realised that rotating objects in three dimensions would require a number system with four dimensions. “An electric circuit seemed to close; and a spark flashed forth… Nor could I resist the impulse – un-philosophical as it may have been – to cut with a knife on a stone of Brougham Bridge, as we passed it, the fundamental formula with the symbols, i,j,k; namely, i2 = j2 = k2 = ijk = –1.” A plaque on the bridge today commemorates this bold inscription of quaternions, a number system with three imaginary axes and one real.
Not all the maths it’s possible to admire on a stroll needs to be this complex. I find flowers beautiful, not just for their shape and colour, but for the mathematical nature of their structure. To encounter these patterns, we only have to wonder: Why does each leaf or petal grow at a certain angle from its neighbour?
All plants contain complex calculations, balancing their exposure to sunlight, moisture, space, energy and interactions with the environment. Leaves form at the apex (tip) of a developing plant as it grows. If each new leaf was to form at an integer multiple of 360° (2π radians), the leaves of a branch would stack on top of one another, blocking lower growth from sunlight and moisture. If a new leaf formed every half rotation, we’d see two rows of stacked leaves. Every one-third rotation would give three rows of stacked leaves, and so on through the fractions.
Some plants may be happy with this simple stacking method, but the plants with big dreams (or the evolutionary path they have followed) have recognised this is not peak efficiency.
Look at a leafy sprig. Turn it in your hands. You can see that to avoid lower leaves lurking in the shadows of those above, the best way for a leaf to form is at an irrational multiple of 360°. Repeating this multiple around the branch would steer clear of overlapping radial lines and give each leaf the best chance to flourish. Pi is an irrational number, as is √2 and infinitely many other numbers which all go on forever and cannot be written as a ratio of two integers. But one number is more irrational than the rest: the golden ratio.
If you have made friends with the right people, then on 22 July each year someone may offer you a slice of pie. This is to celebrate “Pi Approximation Day”, because 22/7 gives 3.142853… – a fairly good approximation of π. Pi’s true rounded value to six decimal places is 3.141592, but the fact it can be approximated so well by a simple fraction means that as far as irrational numbers go, it’s a fairly rational one.
The golden ratio can be mathematically proven to be the most difficult to approximate as a ratio of integers and so it’s the most irrational number – and thus the most efficient path for plants with big ideas.
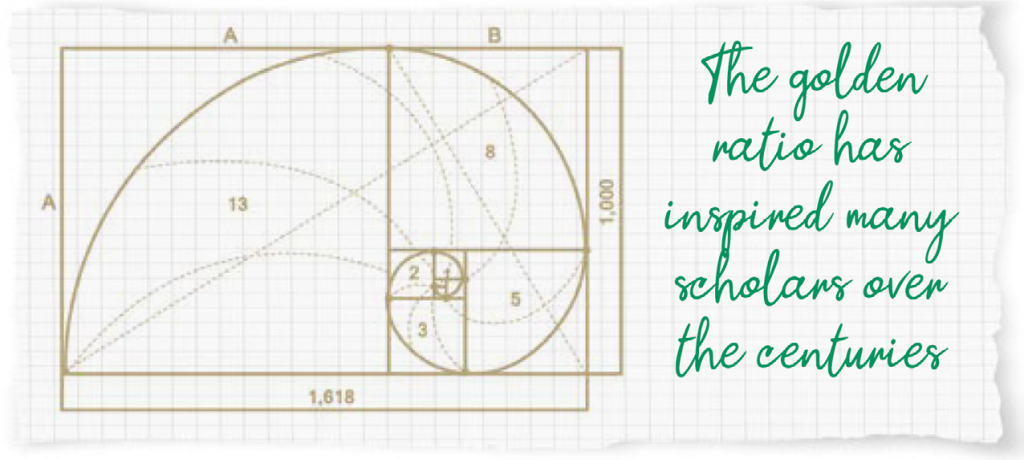
The first known definition of the golden ratio (also called extreme and mean ratio) comes from Euclid’s Elements (c. 300 BCE): “A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.”
Take a line and cut it into a short (lesser) segment of length A and a long (greater) segment B. The total length of the line is A + B. When the ratio of the whole line to the greater segment, (A + B)/B, is equal to the ratio of the greater to the lesser, A/B, the line has been cut according to the golden ratio.
The golden ratio has inspired many scholars over the years, including mathematicians, artists, biologists, architects and musicians. Sir Roger Penrose, awarded a 2020 Nobel Prize in Physics for his work on black holes and general relativity, is also well known for work on Penrose tiles. A simple Penrose tiling consists of two shapes (similar to a dart and a kite) which can tesselate to cover an infinite plane. Like the digits of irrational numbers, this pattern continually changes and never repeats. If you get a chance to count the number of tiles after covering your infinitely large bathroom floor, you will find the ratio of the two types of tiles is the golden ratio.
Related to the golden ratio is the golden angle. The golden angle is the smaller of the two angles created by portioning the circumference of a circle according to the golden ratio. The ratio of the length of the circumference of the circle to the greater arc equals the ratio of the greater to the lesser arc. The golden angle measures 137.5077… degrees and can be considered the most irrational angle – it will never return to its exact original position.
The golden angle often appears in the spacing of leaves on a branch, because it minimises overlap, allowing more sunlight to be captured. The golden angle can also be found in the spacing of seeds on a sunflower head: as the seeds grow radially outward from the centre, this offset reduces empty space between the seeds. The golden ratio is so prevalent in nature it has also been called the divine proportion.
You may be more interested in smelling the flowers than counting angles between leaves, but a simple game of “loves me, loves me not” shows an intriguingly prevalent pattern. Counting petals on each flower, lilies and iris have three main petals, frangipani and hibiscus have five, and it’s common for daisies to comprise eight, 13, 21, 34, 55 or even (for the very patient petal pickers) 89 petals. From this counting exercise the Fibonacci sequence emerges. The Fibonacci sequence was described as early as 200 BCE by Indian mathematicians describing patterns of syllables in Sanskrit poetry. Italian mathematician Leonardo Bonacci, nicknamed Fibonacci, introduced the sequence to Western European mathematics in 1202 through his work studying the population growth of rabbits starting from a single pair.
Each number in the Fibonacci sequence, from the third onward, is obtained by adding together the previous two. The sequence goes on forever and if fn represents the nth term in the sequence it can be expressed (for n≥3): fn= f(n-1) + f(n-2).
There are, of course, some exceptions, but this rule of thumb for petals follows an underlying pattern governing plant growth. If the number of petals on a flower is not a Fibonacci number, it may well be part of the Lucas Numbers: 2, 1, 3, 4, 7, 11, 18, 29, … a sequence also formed by adding successive numbers but starting with different first digits. If you’ve found a flower with one less petal than a Fibonacci or Lucas number, there’s a good chance that one has fallen off.
It’s common to count a Fibonacci number of spirals on pinecones, pineapples, cauliflower and cacti. If your walk leads to the beach, you might be lucky enough to encounter a starfish with Fibonacci-friendly five or eight limbs. An especially plump starfish will trace out the shape of a regular pentagon. The ratio of a diagonal to an edge in a regular pentagon is the golden ratio, one clue that should lead us to suspect a link between the two patterns.
If you take each Fibonacci number and divide it by the previous number, the result gets closer and closer to a certain value:
In the limit as n → infinity, fn/f(n-1) gives 1.618033…, that most irrational irrational, the golden ratio.
Fibonacci himself used the ratio in geometry problems but never recognised its connection to his eponymous sequence. That was noted by Johannes Kepler in 1608, who also said “Geometry has two great treasures: one is the theorem of Pythagoras, the other the division of a line into extreme and mean ratio. The first we may compare to a mass of gold, the second we may call a precious jewel.”
You don’t have to think in four dimensions to be astonished on an afternoon stroll – there are precious jewels of mathematics all around us. Even stopping to smell the flowers can reveal some of nature’s patterns to us, making us glad that the path we follow takes the scenic route.
This article was written by Toby Hendy, lover of phyllotaxis (the arrangement of leaves on a stem) and maths and physics YouTuber (Tibees), for Cosmos Magazine Issue 89.
Illustrations by Phil Constantinesco.
Cosmos magazine is Australia’s only dedicated print science publication. Subscribe here to get your quarterly fill of the best Science of Everything, from the chemistry of fireworks to cutting-edge Australian innovation.
Login or Sign up for FREE to download the educational resources